Parmi les caractéristiques intrinsèques d’un câble ou d’un conducteur, deux valeurs sont essentielles pour son dimensionnement:

Pour les câbles normalisés, ces valeurs sont imposées par la norme, par exemple 90°C et 250°C respectivement pour les câbles isolés au PR/EPR.

Il convient donc de vérifier que le passage du courant de court-circuit (Ik) pendant le temps d’élimination du défaut (t) ne portera pas l’âme du câble au-delà de sa température maximale.

Pour un temps d’élimination du défaut inférieur à cinq secondes (d’où le maximum imposé dans les normes d’installation), l’échauffement est considéré adiabatique, c’est-à-dire que l’on admet que la chaleur produite reste au niveau de l’âme du conducteur et n’a pas le temps de se dissiper dans les autres éléments du câble.

Dans cette hypothèse, la contrainte thermique supportée par les conducteurs se calcule par la formule :

Énergie traversante = Ik² x t en A²s.

La contrainte thermique admissible par le conducteur se calcule par la formule k2 x S2 dans laquelle:

Il convient donc de vérifier que, dans tous les cas de court-circuit la relation soit vérifiée :

Ik² x t < k² x S²

Pour faciliter les calculs, il est possible d’utiliser les tableaux donnant les valeurs de k dans les cas usuels, comme dans l’exemple suivant tiré du document FD C 15-500:

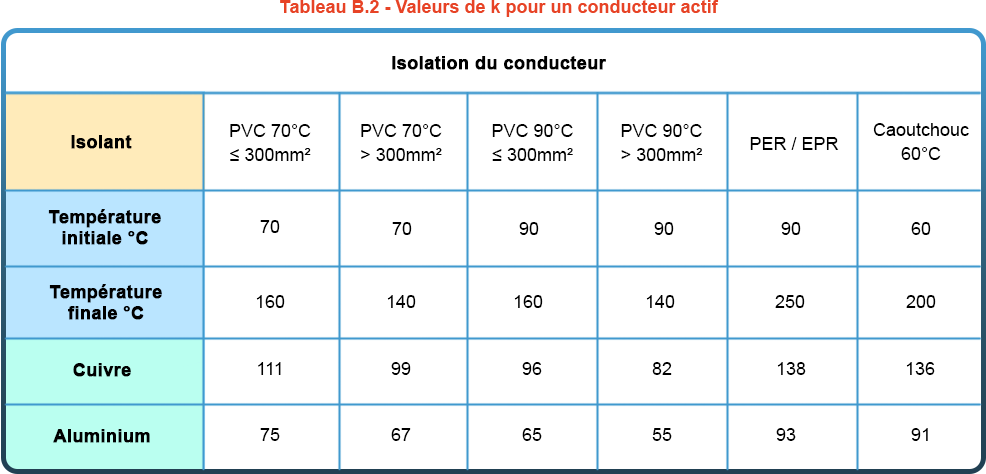
Le logiciel elec calc™ calcule l’énergie traversante maximale sur l’ensemble des conducteurs et vient la comparer à leur tenue thermique (suivant la formule k²xS²). Cette vérification s’applique aux phases mais également au neutre et au PE. Si cette condition n’est pas respectée une erreur de contrainte thermique est affichée sur le câble.

Comment régler un problème de contrainte thermique

En cas de problème de contrainte thermique, il est toujours possible de surdimensionner la section des conducteurs, donc d’augmenter leur contrainte thermique admissible. Néanmoins, d’autres possibilités peuvent permettre de s’affranchir de cette augmentation de section.

Utilisation de fusibles : le temps de fusion d’un fusible est généralement beaucoup plus court que le temps d’ouverture d’un disjoncteur pour des courants de court-circuit élevés. Il y a donc une limitation naturelle de l’énergie traversante. A noter qu’en cas de protection par fusible, l’énergie maximale peut avoir lieu lors du court-circuit minimal car le temps de fusion peut-être plus grand. Il est donc nécessaire de vérifier la tenue du câble pour tous les types de courant de court-circuit.

Utilisation de disjoncteurs limiteurs : certaines gammes de matériels sont conçues pour empêcher l’établissement du courant de défaut, en ne laissant passer qu’un courant d’intensité limitée. La performance de limitation d’un disjoncteur est donnée par le constructeur sous forme de courbes de limitation:

Le catalogue multi-fabricant d’elec calc™ gère les courbes de limitation des différentes protections. Dès lors qu’une référence matériel disposant d’une limitation est associée à une protection, le logiciel va pouvoir récupérer l’énergie limitée associée au courant de court-circuit présumé.

A noter que la plupart des disjoncteurs modulaires disposent de capacités de limitation, permettant de solutionner les problèmes de contrainte thermique dans les canalisations de faible section qui sont le plus affectées par les problèmes de contrainte thermique.

Exemple :

Mon installation comporte un circuit d’éclairage avec un câble U1000R2V-3G2.5 protégé par un disjoncteur 16 A courbe C. Le courant de court-circuit maximal au niveau du câble est de 5.63 kA et le temps de déclenchement de la protection 10 ms.

L’énergie maximale est donc : Ik² x t = 5.63²x0.01, soit 316 969 A²s
La tenue thermique de mon câble est : k² x S² = 138²x2.5², soit 119 025 A²s

Vérification : Ik² x t > k² x S² => problème de contrainte thermique sur le câble: en cas de court-circuit le câble sera endommagé.

Cas du fusible :

Si je remplace le disjoncteur par un fusible gG de calibre 16 A, le temps de fusion est de 4.10-5s.
L’énergie maximale est donc : Ik² x t = 5.63²x0.00004, soit 1268 A²s
Il n’y a donc pas de problème de contrainte thermique sur le câble.
Dans notre cas , nous avons également vérifié que c’est bien le courant de court-circuit maximal qui donne l’énergie maximale.

Intégration d’une référence disjoncteur avec limitation :

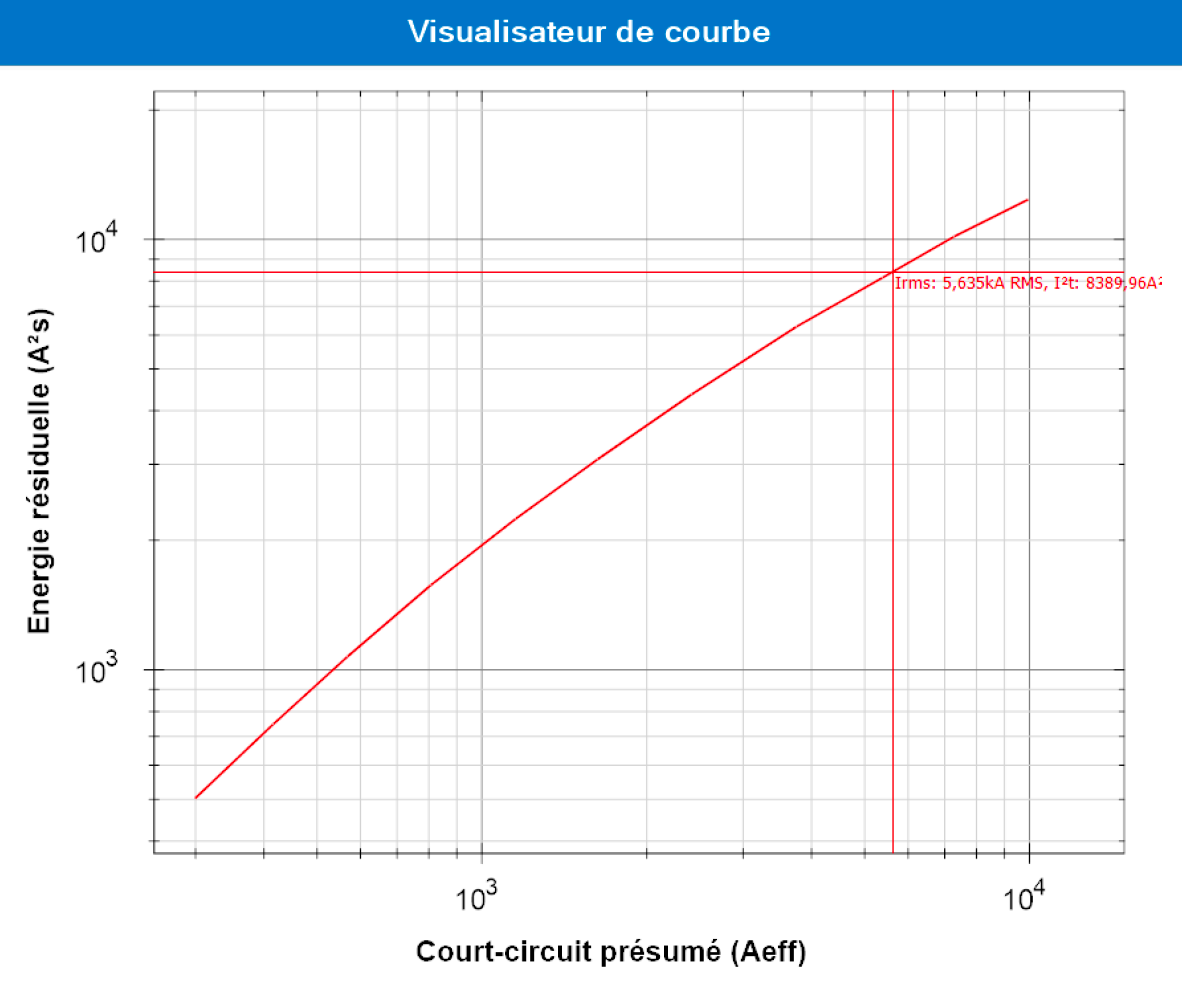
J’intègre maintenant une référence matériel sur ma protection. Le logiciel va donc pouvoir lire sur la courbe de limitation en énergie fournie par le fabricant l’énergie résiduelle pour un courant de circuit de 5.63kA :

Dans notre cas l’énergie résiduelle est de 8 389 A²s. Elle est inférieure à la tenue thermique du conducteur. Nous n’avons donc plus de problème de contrainte thermique sur le câble.

Prise en compte de la composante continue : dans les formules citées ci-dessus, nous avons considéré que la valeur de Ik est la valeur efficace de la composante alternative du courant présumé de défaut. Si l’on veut être plus précis, il faut tenir compte de la composante continue du courant de défaut. L’influence de cette composante continue est surtout sensible lorsque le point de défaut est proche des sources. Elle dépend du temps d’élimination du défaut et de la valeur du rapport X/R du circuit au point de défaut. Il convient alors de calculer un courant thermique équivalent qui remplace dans les
formules le courant Ik.

elec calc™ prend en compte l’influence de cette composante continue lorsque la norme utilisée l’impose.

Cas des sources multiples : un défaut peut être alimenté par plusieurs sources contribuant chacune au courant de court-circuit. Les protections associées à ces différentes sources peuvent ne pas réagir dans le même temps au courant de court-circuit qu’elles génèrent. Le calcul précis de l’énergie traversante doit donc intégrer un cumul chronologique des énergies produites par chaque source.

C’est ce que réalise le logiciel elec calc™ afin de s’approcher au plus près du phénomène réel.