Van de intrinsieke eigenschappen van een kabel of geleider zijn twee waarden essentieel voor de dimensionering:

Voor gestandaardiseerde kabels worden deze waarden opgelegd door de norm, bijvoorbeeld respectievelijk 90°C en 250°C voor PR/EPR geïsoleerde kabels.

Daarom moet worden gecontroleerd of de doorgang van de kortsluitstroom (Ik) tijdens de foutopruimingstijd (t) er niet toe leidt dat de kabelkern zijn maximumtemperatuur overschrijdt.

Voor een storingverwijderingstijd van minder dan vijf seconden (vandaar het maximum dat wordt opgelegd in de installatienormen) wordt de verwarming als adiabatisch beschouwd, d.w.z. er wordt aangenomen dat de geproduceerde warmte in de kern van de geleider blijft en geen tijd heeft om naar andere delen van de kabel te dissiperen.

In dit geval wordt de thermische spanning op de geleiders berekend met de formule :

Doorgaande energie = Ik² x t in A²s.

De toelaatbare thermische spanning van de geleider wordt berekend met de formule k2 x S2, waarbij

Daarom moet worden gecontroleerd of in alle gevallen van kortsluiting de relatie wordt geverifieerd:

Ik² x t < k² x S²

Om de berekeningen te vergemakkelijken, kunnen de tabellen met de waarden van k in de gebruikelijke gevallen worden gebruikt, zoals in het volgende voorbeeld uit document FD C 15-500:

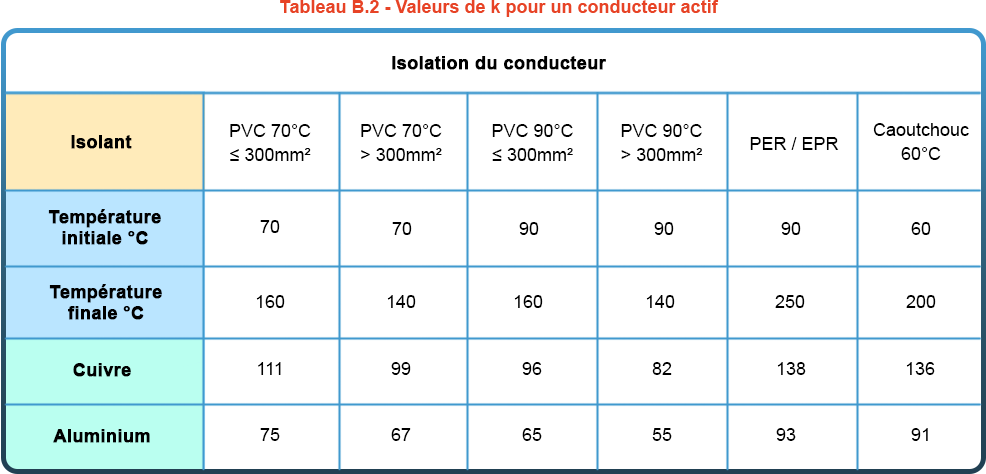
De elec calc™ software berekent de maximale energie die door alle geleiders gaat en vergelijkt deze met hun thermische weerstand (volgens de formule k²xS²). Deze controle is niet alleen van toepassing op de fasen, maar ook op de nulleider en PE. Als niet aan deze voorwaarde wordt voldaan, wordt een thermische stressfout weergegeven op de kabel.

Hoe een thermisch stressprobleem oplossen

In het geval van een probleem met thermische spanning is het altijd mogelijk om de doorsnede van de geleider te vergroten, waardoor de toelaatbare thermische spanning toeneemt. Er zijn echter andere manieren om deze vergroting van de doorsnede te vermijden.

Gebruik van zekeringen: de smelttijd van een zekering is over het algemeen veel korter dan de openingstijd van een stroomonderbreker voor hoge kortsluitstromen. Er is dus een natuurlijke beperking van de doorgelaten energie. Er moet worden opgemerkt dat bij zekering de maximale energie kan optreden tijdens de minimale kortsluiting omdat de smelttijd langer kan zijn. Daarom moet de weerstand van de kabel tegen alle soorten kortsluitstromen worden gecontroleerd.

Gebruik van stroombegrenzende vermogensschakelaars: bepaalde series apparatuur zijn ontworpen om te voorkomen dat de foutstroom zich opbouwt, door alleen een stroom van beperkte intensiteit door te laten. De limietprestaties van een vermogensschakelaar worden door de fabrikant opgegeven in de vorm van limietcurves:

De multifabrikantencatalogusvan elec calc™ beheert de begrenzingscurves van de verschillende beveiligingen. Zodra een hardwarereferentie met een beperking is gekoppeld aan een beveiliging, kan de software de beperkte energie terugwinnen die is gekoppeld aan de veronderstelde kortsluitstroom.

Opgemerkt moet worden dat de meeste modulaire vermogensschakelaars een begrenzend vermogen hebben, waardoor het mogelijk is om thermische spanningsproblemen op te lossen in leidingen met een kleine doorsnede, die het meest onder thermische spanningsproblemen te lijden hebben.

Voorbeeld:

Mijn installatie heeft een verlichtingscircuit met een U1000R2V-3G2.5 kabel die wordt beveiligd door een 16 A stroomonderbreker. De maximale kortsluitstroom op de kabel is 5,63 kA en de uitschakeltijd van de beveiliging is 10 ms.

De maximale energie is dus :
Ik² x t = 5,63²x0,01, d.w.z. 316.969 A²s De warmteweerstand van mijn kabel is: k² x S² = 138²x2,5², d.w.z. 119.025 A²s

Controle: Ik² x t > k² x S² => probleem van thermische spanning op de kabel: bij kortsluiting wordt de kabel beschadigd.

Zekering :

Als ik de stroomonderbreker vervang door een gG-zekering van 16 A, is de smelttijd 4,10-5s. De maximale energie is dus :

Ik² x t = 5,63²x0,00004, d.w.z. 1268 A²s Er is dus geen probleem van thermische spanning op de kabel. In ons geval hebben we ook gecontroleerd dat het de maximale kortsluitstroom is die de maximale energie geeft.

Integratie van een stroomonderbrekerreferentie met beperking :

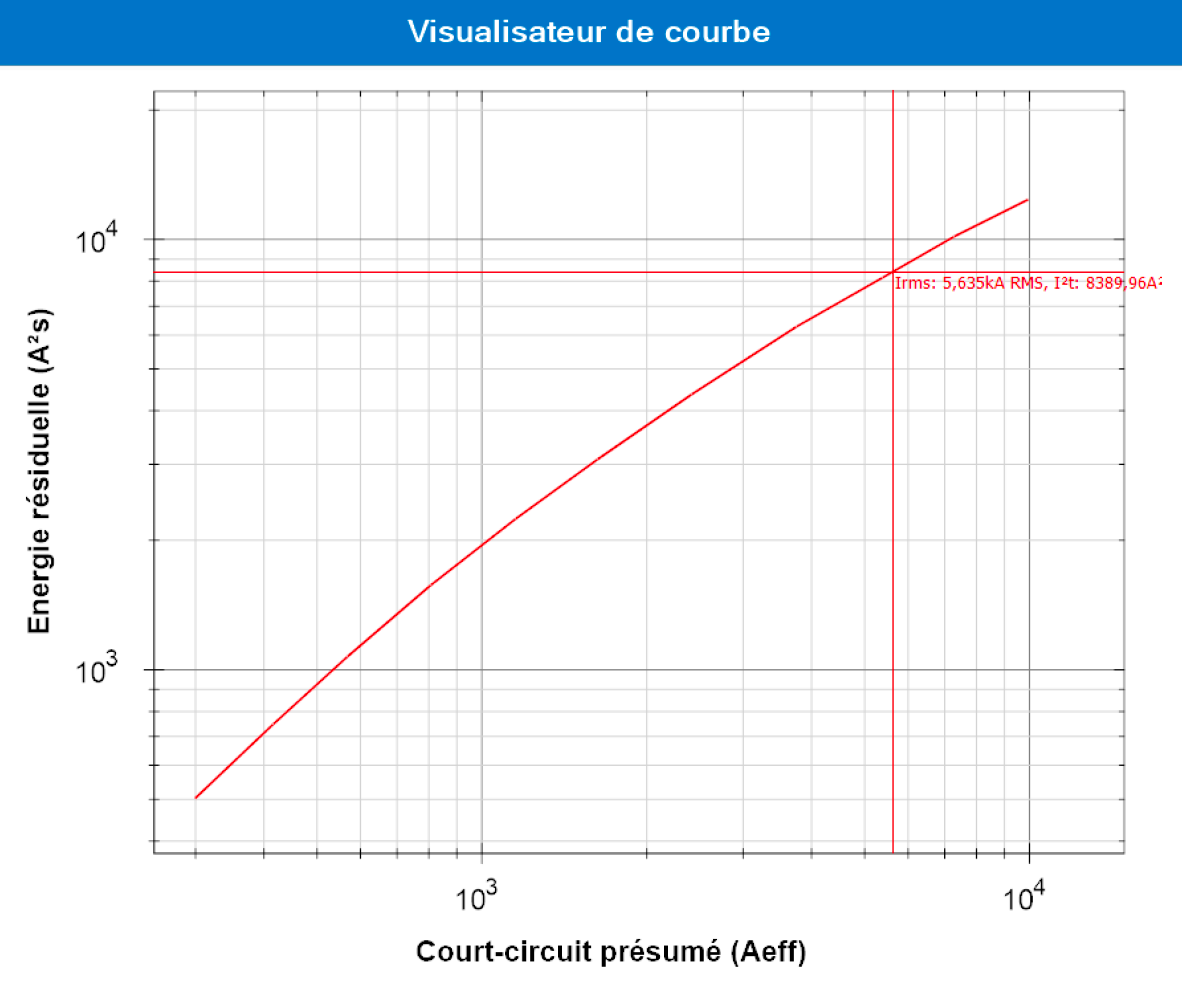
Ik integreer nu een hardwarereferentie op mijn beveiliging. De software zal dus in staat zijn om de restenergie voor een circuitstroom van 5,63 kA af te lezen uit de energiebeperkingscurve die door de fabrikant wordt geleverd:

In ons geval is de restenergie 8.389 A²s. Dit is minder dan de thermische weerstand van de geleider. We hebben dus geen probleem meer met thermische spanning op de kabel.

Rekening houden met de DC-component: in de bovenstaande formules hebben we aangenomen dat de waarde van Ik de RMS-waarde is van de AC-component van de veronderstelde foutstroom. Als we nauwkeuriger willen zijn, moeten we rekening houden met de DC-component van de foutstroom. De invloed van deze DC-component is vooral merkbaar als het foutpunt zich dicht bij de bronnen bevindt. Deze is afhankelijk van de foutopruimingstijd en de waarde van de X/R-verhouding van het circuit op het foutpunt.
Het is dan nodig om een equivalente thermische stroom te berekenen die de stroom Ik in de formules vervangt.

elec calc™ houdt rekening met de invloed van deze DC-component als de gebruikte norm dit vereist.

Geval van meerdere bronnen: een fout kan worden gevoed door meerdere bronnen, die elk bijdragen aan de kortsluitstroom. Het is mogelijk dat de beveiliging van deze verschillende bronnen niet tegelijkertijd reageert op de kortsluitstroom die ze genereren. De nauwkeurige berekening van de energie die doorstroomt, moet daarom een chronologische opeenstapeling van de energieën bevatten die door elke bron worden geproduceerd.

Dit is wat de elec calc™ software doet om het echte fenomeen zo dicht mogelijk te benaderen.